X-rays can be reflected under certain conditions when hitting matter. Mostly three reflection types are distinguished:
| Total external reflection | Bragg reflection | Multi layer reflection |
Total external reflection
When X-rays enter matter under grazing incidence, they will be reflected by Total External Reflection (TER) when the angle of incidence is below the critical angle αcritical.
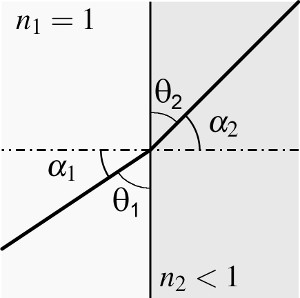
Fig. 1: Sketch showing the angles and indices of refraction used
to calculate the critical angle of total external reflection
The critical angle can be calculated as follows (see fig. 1). From the refraction of X-rays we know that Snell's law is
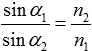
with the angle α1 of the incoming ray and α2 of the outgoing ray and the indices of refraction n2 in matter and n1 in the medium the ray comes from. Total external reflection occurs for angles α1, when the angle α2 reaches 90°. Assuming the ray comes from vacuum, n1=1. So the critical angle αcritical is
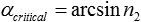
As n2 is only slightly below one (for example for gold for photon energies of 12.4 keV, n2 = 1-1.88·10-5), the maximum angle for TER to occur is close to 90° (for gold at 12.4 keV αcritical = 89.65° = 90°-0.351°). For X-rays total external reflection occurs only under grazing incidence. So the reflection angles α are always close to 90°. Consequently normally the reflection angles are measured as angles θ between the incoming ray and the mirrors surface. The critical angle θcritical is then
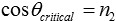
with n2 = 1-δ and with the Taylor expansion of the cosine
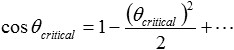
the critical angle θcritical is
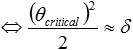
or
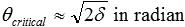
or when multiplying with 180/π
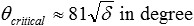
This approximation results in an error below 0.021% for θcritical<1°. In the example of gold and a photon energy of 12.4 keV, θcritical =0.351°. Total external reflection is nearly, but not completely loss-less, because the absorption coefficient β is not zero.
Bragg reflection
Crystal surfaces show high reflectivity under special angles depending on the wavelength of the X-rays due to Bragg-reflection. Mirrors using Bragg-reflection to redirect X-rays are called crystal mirrors. These mirrors provide large reflection angles when the reflection condition for a given wavelength is fulfilled. To understand the physical principle, the path difference of an incoming ray reflected at the surface of a crystal and a neighbour ray being reflected at the next inner atomic layer is regarded (see fig. 2). When the optical path difference
Δ=2d sinθ
with the distance d between two adjacent atomic layers and the angle θ of the incoming wave measured to the surface is an integer multiple m of the wavelength λ, constructive interference occurs and consequently the wave is reflected. This is known as Bragg equation:
mλ=2d sinθ
Bragg reflection is used for example to focus monochromatic light with e.g. elliptically curved crystal mirrors and in monochromators to filter wavelengths and in material science when calculating the atomic lattice constants d from the reflection angles at crystalline samples.
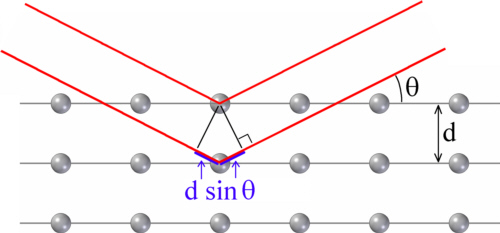
Fig. 2: Bragg reflection; when die optical path difference Δ=2d sinθ for a certain wavelength λ is a multiple of λ, the beams will interfere constructively.
Multi layer reflection
An X-ray mirror can be formed by fabricating a multi layer system consisting of layers of different index of refraction (see fig. 3).
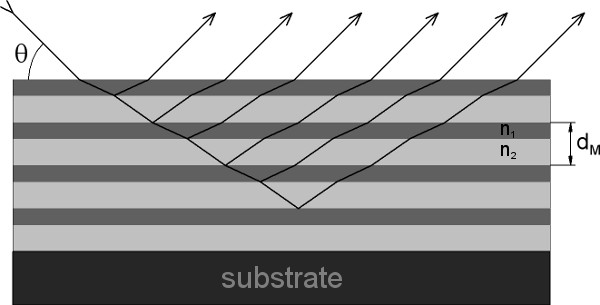
Fig. 3: X-ray reflection at a multi layer mirror
The Bragg equation then changes to compensate for the refraction in the layers [Tho 2009]:
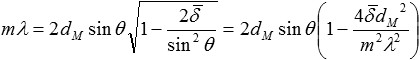
with the order m, the wavelength λ, the period dM of the multi layer system, the angle of incidence θ and the real part ![]() of the period-averaged index of refraction of the multi layer system.
of the period-averaged index of refraction of the multi layer system.
| [Tho 2009] |
A. C. Thompson, J. Kirz, D. T. Attwood, E. M. Gullikson, M. R. Howells, J. B. Kortright, Y. Liu and A. L. Robinson; X-ray data booklet, third edition, Lawrence Berkeley National Laboratory, Berkeley, California, 2009 |


